Определение наиболее важного узла в сети
АБН: Определение наиболее важного узла в сети
Определение наиболее важного узла в сети
Грызунов В.В., начальник отдела тестирования
ЗАО "Удостоверяющий Центр"
На сегодняшний момент очень сложно найти отрасль человеческой деятельности, которую миновал бы процесс информатизации. Вместе с тем, создаваемые информационные системы (ИС) становятся, во-первых, сильно разветвленными и разнородными, во-вторых, открытыми. Оба перечисленных фактора довольно жестко ставят вопросы безопасности обрабатываемых в ИС данных. Здесь возникает ряд вопросов. Вот только часть из них: какие именно из существующих в ИС объектов надо защищать? Насколько сильно защищать? Что является критическим ресурсом в ИС? Где размещать средства контроля? При этом стоимость систем защиты информации (СЗИ) довольно высока и правильный их выбор и настройка поможет не только достигнуть требуемого уровня защищенности ИС, но и сделать это максимально дешево.
Помочь ответить на обозначенные вопросы и призван предложенный в статье метод определения наиболее важного узла (сегмента, участка) сети, т.е. тех ресурсов сети, которые имеет смысл защищать. Эта информация будет тировщикам, если СЗИ разрабатывается для конкретного заказчика, так и эксплуатирующим и администрирующим ИС людям, если СЗИ собирается из готовых продуктов и настраивается для конкретной ИС.
В общем случае для каждой конкретной ИС существует несколько различных критериев определения важности узлов, которые применительно к ИС условно можно разбить на объективные и субъективные. К объективным, не зависящим от качества обрабатываемой информации, можно отнести, например, топологическую значимость узла сети (маршрутизатора, сервера и т.д.), направление и плотность информационных потоков, проходящих через узел и т.д. К субъективным, зависящим от качества передаваемой информации, принадлежат, например, важность обрабатываемой информации, определение критичных по разным показателям маршрутов и путей прохождения информации и т.п.
Иными словами, при ранжировании узлов сети по степени важности необходимо учитывать несколько критериев, а сама задача определения наиболее важного участка в сети видится как многокритериальная.
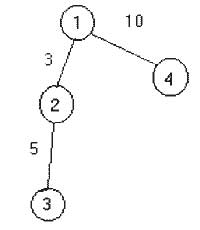
Рис.2. Множество альтернатив
Для ее решения представим сеть в виде неориентированного взвешенного графа (рис. 1). В общем случае количество критериальных функций может быть любым. Однако мы упростим задачу выбора узла и предположим, что нам интересны только два критерия важности узлов сети: количество путей, проходящих через узел, и сумма весов входных и выходных дуг. Покажем на этом примере, как производится выбор наиболее важного участка сети предложенным нами методом. В его основе лежит покомпонентное лексикографическое построение результирующего отношения предпочтения, суть которого в следующем.
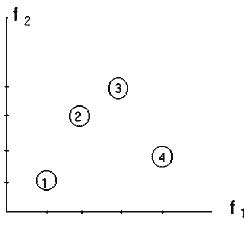 Рис. 1. Модель сети в виде неориентированного взвешенного графа
Рис. 1. Модель сети в виде неориентированного взвешенного графа
- Поскольку в нашем примере рассматриваются только две критериальные функции, то введем двумерное пространство f1хf2 (рис. 2).
- Произведем ранжирование узлов сети по степени важности согласно первой критериальной функции f1. Для этого подсчитаем количество путей, проходящих через вершины графа. Расставим приоритеты вершин и отсортируем их по важности согласно критериальной функции f1. (табл. 1). Расположим по оси f1 вершины по убыванию их приоритета.
- Произведем ранжирование узлов сети по степени важности согласно второй критериальной функции f2. Для этого подсчитаем сумму весов входных и выходных дуг каждой вершины, расставим приоритеты и отсортируем вершины (табл. 2). "Поднимем" уже расположенные по оси f1 вершины на величину их приоритета по оси f2 (рис. 2).
- Предположим, что нам интересен случай, когда наши критериальные функции стремятся к минимуму и произведем непосредственно выбор наиболее важного участка сети. В общем случае возможны три варианта.
- f1, f2 не доминируют друг друга и принадлежат множеству Парето. В этом случае вершины в порядке снижения приоритета будут упорядочены так: 1, 2, 4, 3. Поверхность уровня перпендикулярна биссектрисе начала координат;
- f1 доминирует f2. (1, 2, 3, 4). Поверхность уровня параллельна оси f2;
- f2 доминирует f1. (1, 4, 2, 3). Поверхность уровня параллельна оси f1;
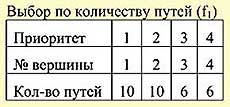 Таблица 1 Таблица 1 |
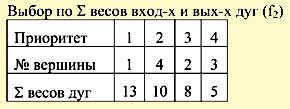 Таблица 2 Таблица 2 |
Для того, чтобы показать общность метода, в примере были выбраны субъективная и объективная критериальные функции. Используя субъективные критериальные функции, на наш взгляд, имеет смысл их нормировать. В заключении добавим, что случай из n критериальных функций отличается от описанного только тем, что пространство будет не двумерным, а n-мерным.
Таким образом, в данной статье представлен один из подходов к определению тех ресурсов сети, которые необходимо не просто защищать, а защищать наилучшим образом и в первую очередь, что позволит разделить требования по безопасности к защищаемым объектам, грамотно установить и оправданно снизить затраты на всю систему защиты ИС.
Статья предоставлена порталом о Радиоэлектронике и Телекоммуникациях www.informost.ru
и новости компании